이 내용은 임석구, 홍경호의 ‘Modern Computer Architecture’를 참고하였습니다.
1. 논리 게이트
2. 화재 대수학
1. 논리 게이트
TTL 대 CMOS 로직 레벨 정의
TTL: 논리 1(2.5~5V), 논리 0(0~0.8V)
CMOS : 로직 1(3.5~5V), 로직 0(0~1.5V)
1) NOT 게이트
– 인버터라고도 합니다.
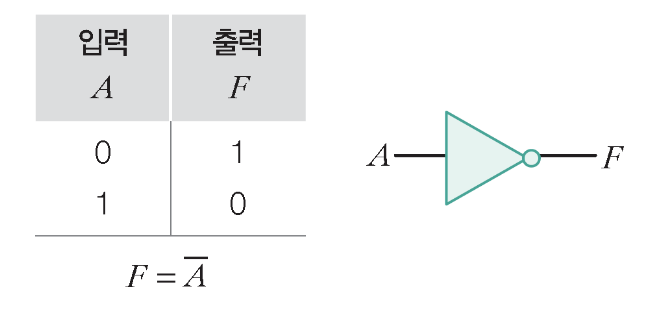
2) 버퍼 게이트
– 간단한 전송
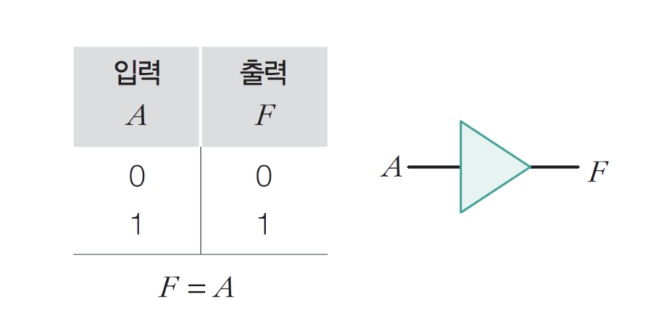
4) 3상태 버퍼 게이트
– 출력이 하이, 로우, 하이 임피던스 중 하나인 게이트
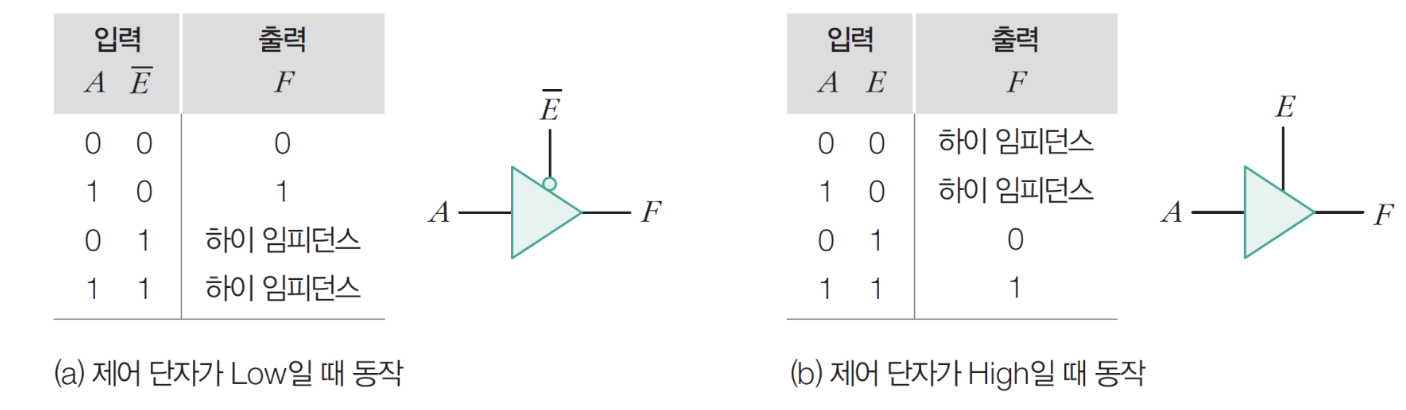
5) AND 게이트
– 모든 입력이 1인 경우 1출력
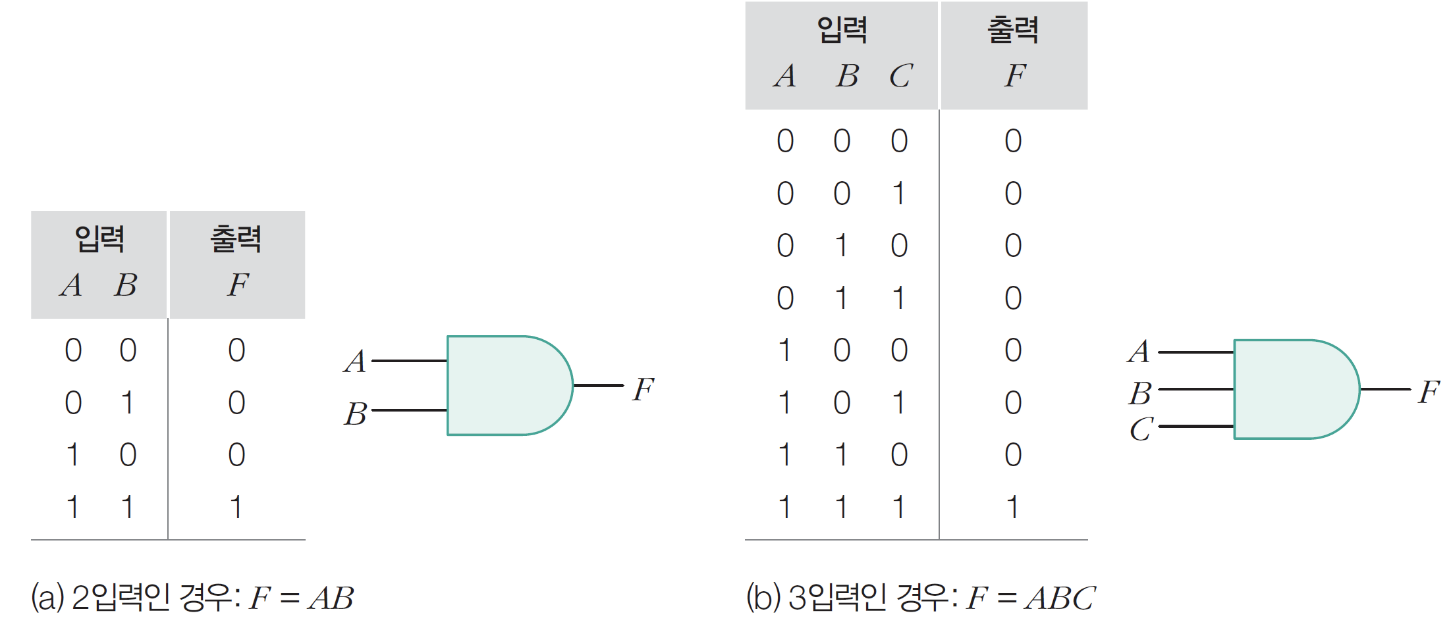
6) OR 게이트
– 입력이 하나라도 1이면 출력은 1
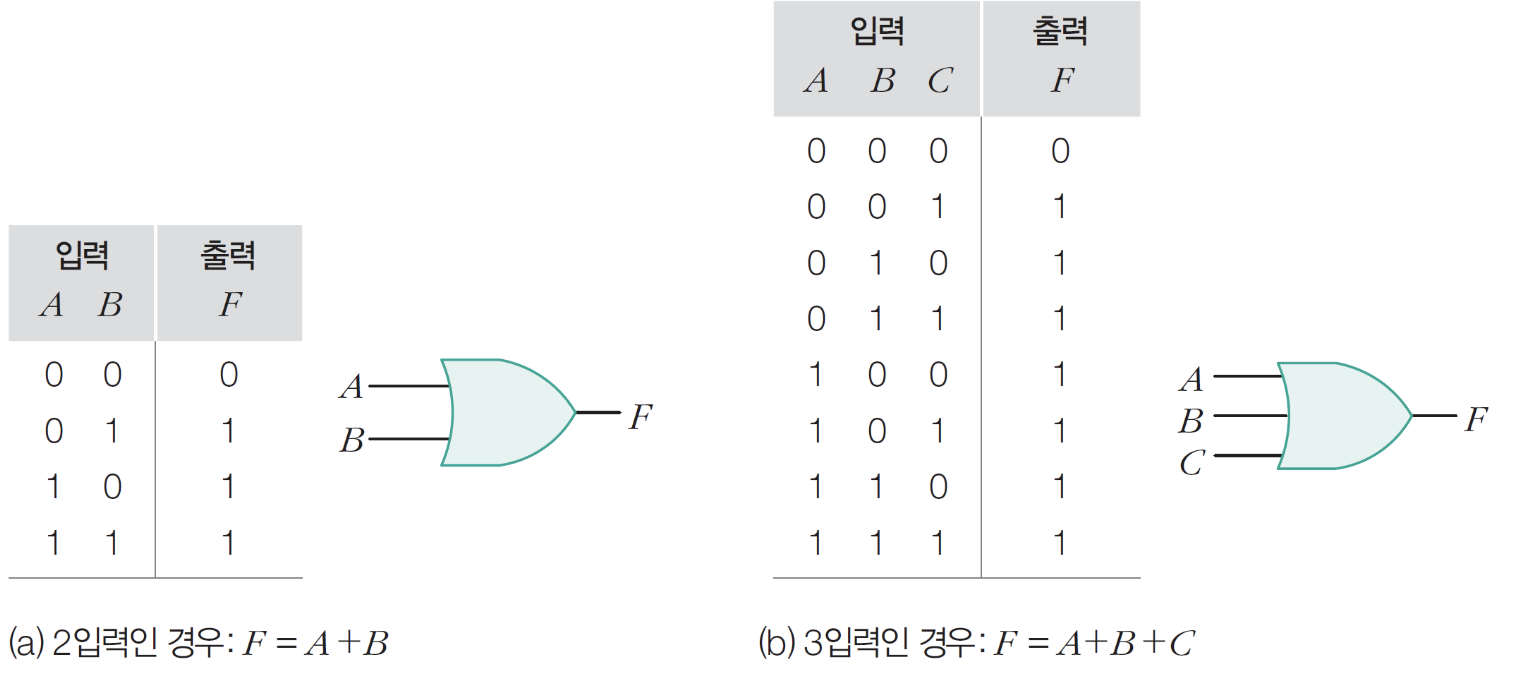
7) 낸드 게이트
– 모든 입력이 1이면 출력은 0
– AND + NOT
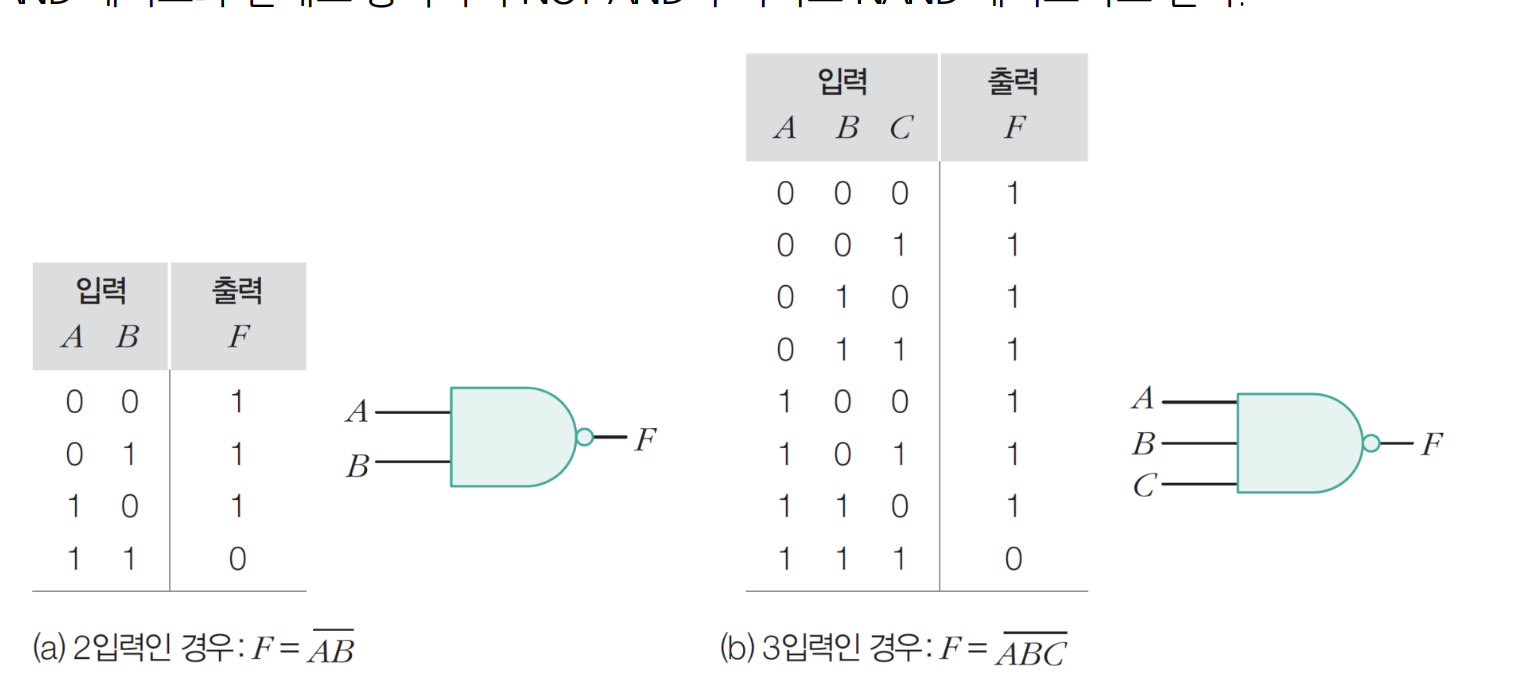
8) NOR 게이트
– 입력이 하나라도 1이면 출력은 0
– 또는 + 아님
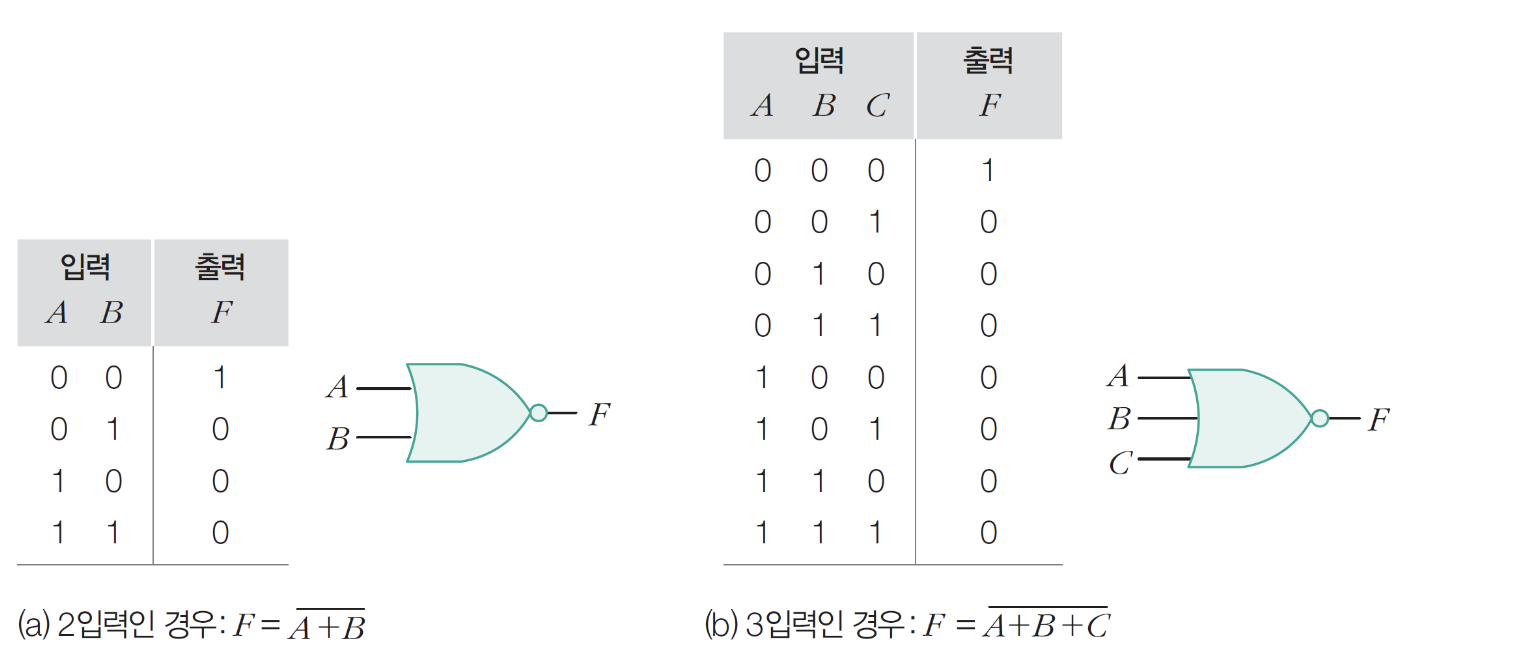
9) XOR 게이트
– 1이 홀수이면 1, 짝수이면 0
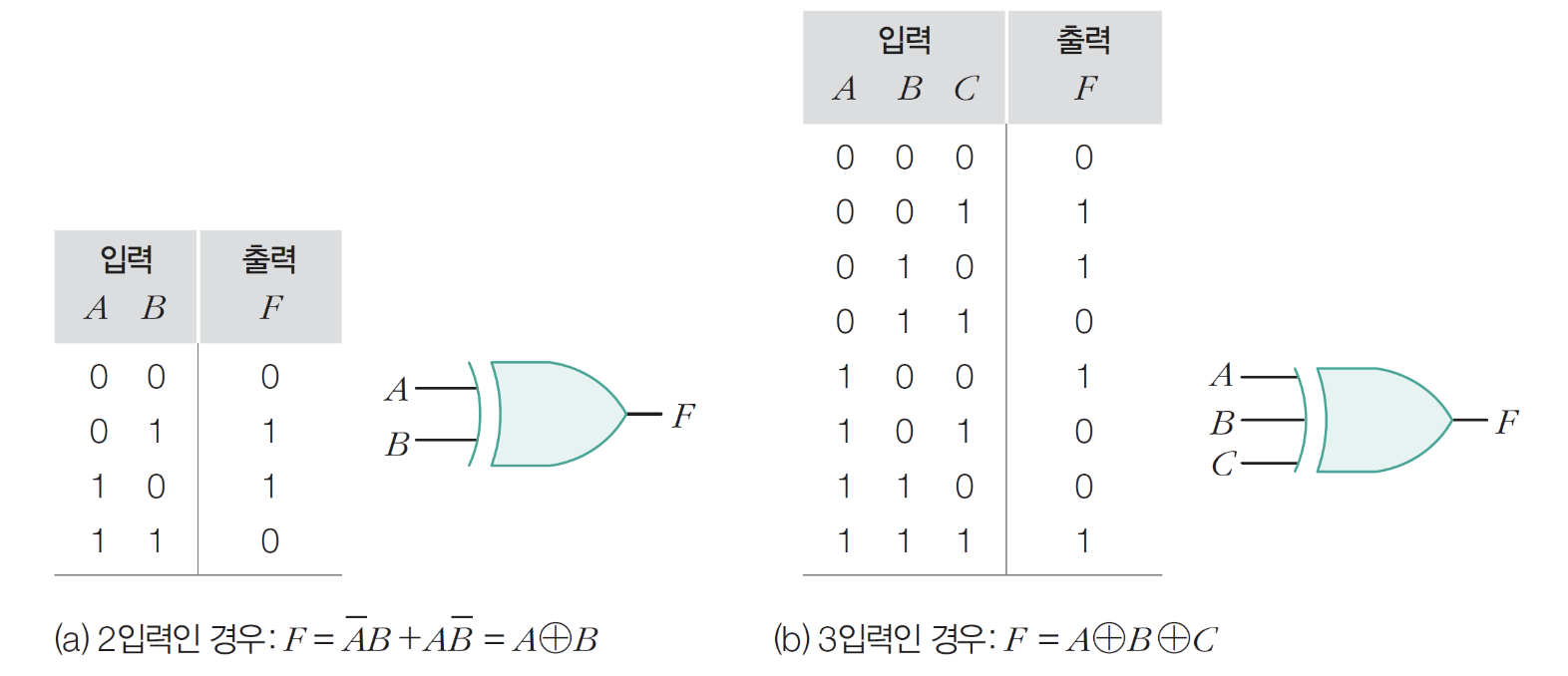
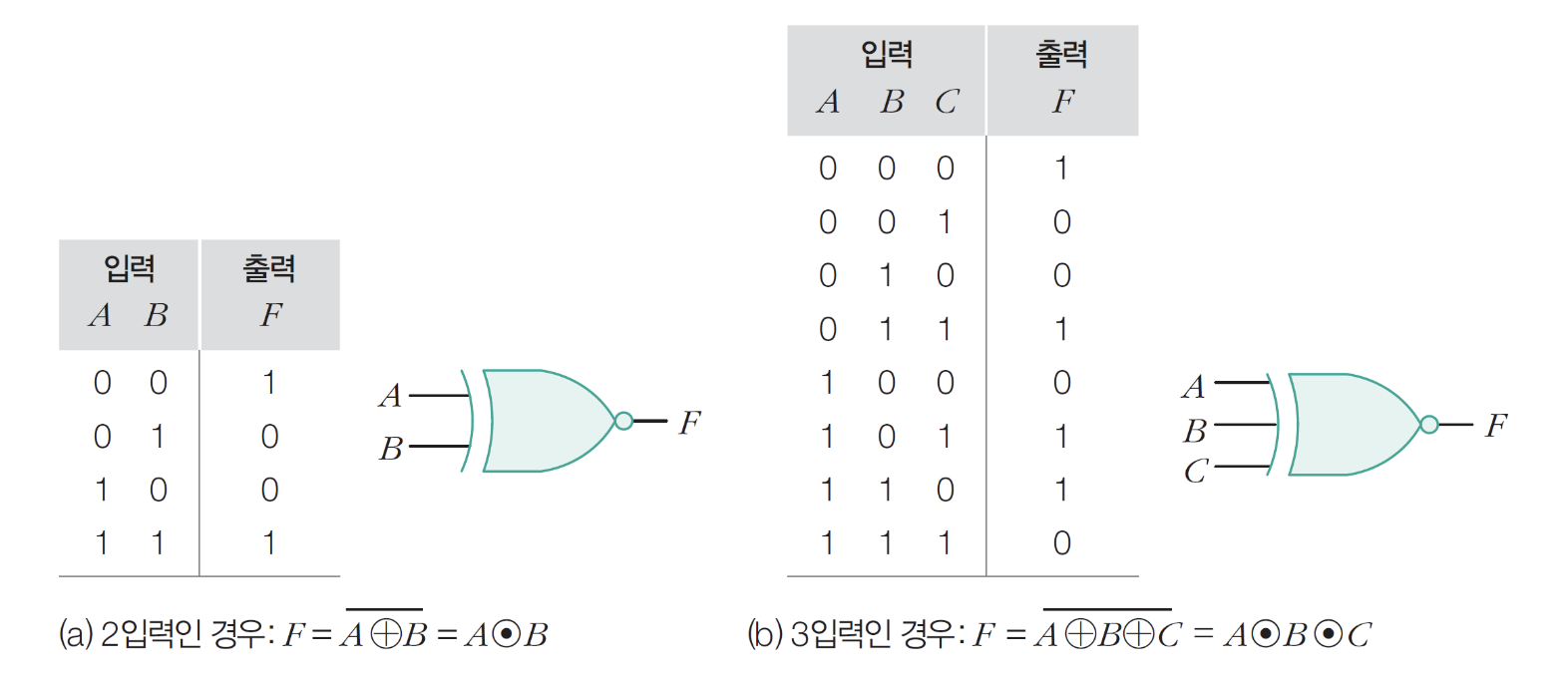
10) XNOR 게이트
– 1이 홀수이면 0, 짝수이면 1
– XOR + NOT
11) 유니버설 게이트
– 모든 회로는 NAND 게이트와 NOR 게이트만으로 구성할 수 있으므로 이 두 게이트를 범용 게이트라고 합니다.
11-1) NOT 게이트
– NOT 게이트는 NAND 또는 NOR 게이트의 입력을 결합하여 만들 수 있습니다.

11-2) AND 게이트
– F = AB에서 이중 부정 솔루션 구현
-> AB = (A’+B’)’ = AB
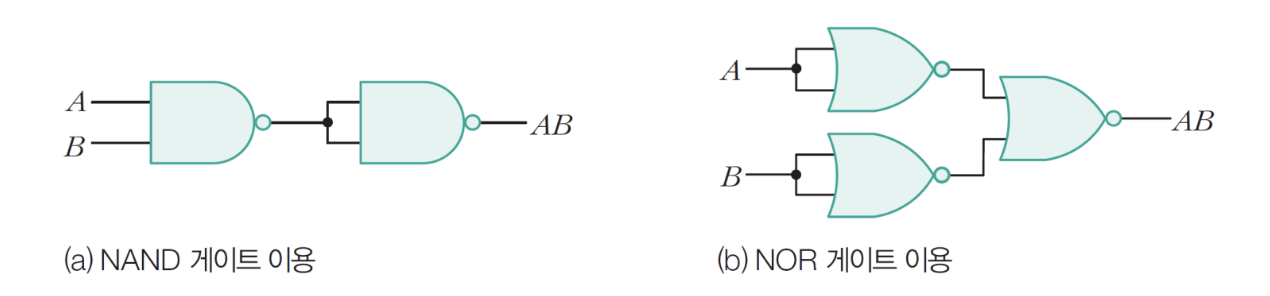
11-3) OR 게이트
– F = A + B에서 이중 부정 솔루션 구현
-> A+B = (A’B’)’ = A+B
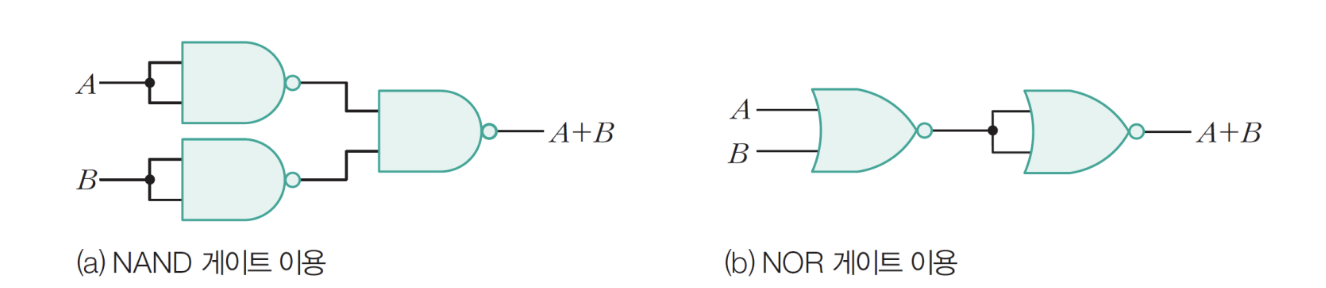
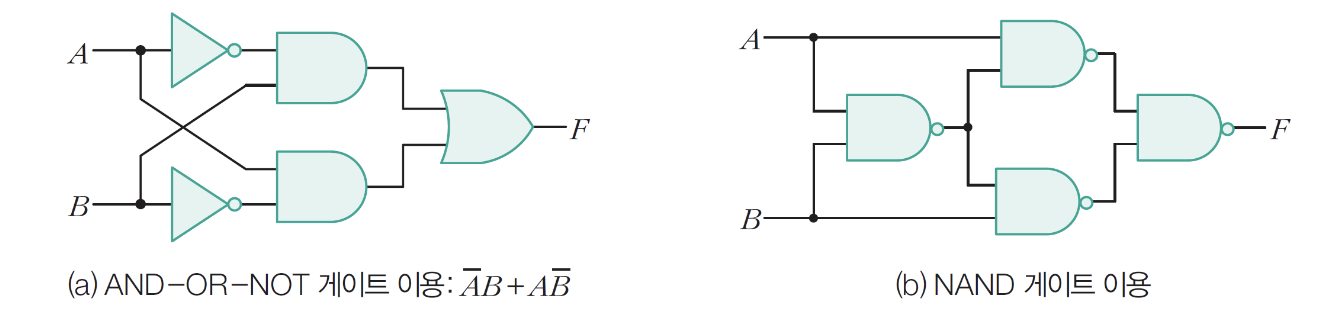
11-4) XOR 게이트
12) 유선 로직
– 집적회로(IC)에서는 NAND 게이트와 NOR 게이트로 구성된다.
– 2개 이상의 NAND 또는 NOR 연결 게이트의 출력에 연결하여 특정 논리 기능을 수행하는 형태를 유선 논리라고 합니다.
2. 화재 대수학
– AND, OR, NOT을 이용하여 대수식을 표현합니다.
– 그리고 : x
– 또는 : +
– NOT : A’
– 기본적으로 교환 및 조합이 적용됩니다.
– 증명은 진리표로 증명한다.
분배 법칙
– A+BC = (A+B)(A+C)
-A(B+C) = AB + AC
드 모건의 정리
(A+B)’ = A’B’
(AB)’ = A’+B’
흡수 법칙
A + AB = A
A(A+B) = A
합의 정리
AB + BC + A’C = AB + A’C
(A+B)(B+C)(A’+C) = (A+B)(A’+C)
공 대수식의 표현 형태
1) 제품과 minterm의 합계
1-1) 제품 합계
– 1단계 입력은 AND를 의미하고, 2단계 입력은 OR로 구성된 논리식을 의미합니다.
1-2) 민텀
– 기호로 00, 01, 10, 11을 입력합니다.
– 입력이 0이면 NOT으로 표현
00 – A’B’
01 – A’B
10 – AB’
11 – AB
1-3) 최소항식
– 출력이 1인 항의 변수를 AND 연산하고 각 항의 OR 연산을 표현한 것입니다.

2) 합계와 최대 항의 곱
2-1) 합계의 곱셈
– 1단 입력이 OR이고 2단 입력이 AND인 논리식.
2-2) 최장기한
– 기호로 00, 01, 10, 11을 입력합니다.
– 민텀의 반대말
– 입력값이 1이면 NOT으로 표현
00 – A+B
01 – A+B’
10 – A’+B
11 – A’+B’
2-3) 최대 용어 표현
– 출력이 0이 되는 입력 변수를 OR 처리한 후 AND 처리하는 방식입니다.

정리하다
– 가장 큰 항과 가장 작은 항은 서로 보완적이다. (서로 부정적인 관계)
논리식의 단순화
1) 공 대수학 법칙을 사용하십시오.
2) Karnaugh 맵을 사용합니다.
3) 다이어그램 방법을 사용하십시오.
카르노 지도
– minterms를 사용합니다. (입력값이 0이면 NOT으로 표현)
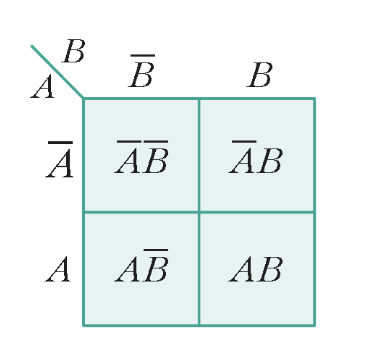


규칙
1. 인접한 민텀을 함께 그룹화합니다.
2. 번들 단위는 1, 2, 4, 8, 16 단위로 그룹화됩니다.
3. 직선, 정사각형, 사선은 불가능합니다.
4. 최대한 크게 묶는다.
5. 중복 결속이 간단하면 이중 결속.
6. 관련 없는 용어를 단순화할 수 있는 경우 묶습니다. 그렇지 않으면 연결되지 않습니다.
무관한
– 입력값이 0이든 1이든 상관없다. 즉 최소항은 결과에 영향을 미치지 않는다.
– x 또는 d로 표시
XOR 및 XNOR의 카르노 맵
– Karnaugh map에서 grouping되어 제거된 변수들 외의 입력변수들 중 1의 개수가 홀수이면 XOR, 짝수이면 XNOR.